ベイジアン、ベイズ統計、ベイズ理論、最近なんだかよく聞く言葉です。
Intel、過去の経験を分析し次の一手を考えるソフトウェアを公開OpenMLは、「ベイズ理論」を使い、次に起こることを予測する。音声認識や読唇からの言語認識、人工知能、データ分析、遺伝子配列分析、故障診断、など様々なアプリケーションに使うことが可能で、計算機分野ではアプリケーションランタイムの最適化などへの使用が考えられる。
グーグル、インテル、MSが注目するベイズ理論:今日のコンピュータ界を動かす18世紀の確率論サーチエンジン超大手のGoogleと情報検索ツールを販売するAutonomyの両社もベイズの原理を採用し、百発百中ではないにしろ高い確率で適当なデータを探し当てる検索サービスを提供している。
確率論のひとつで、しかもかなりの古典。その古典がなぜ今注目されているのか?そのヒミツがここ最近のコンピューティング能力の劇的な向上があるのでしょう。高い計算能力をもつCPUとデータを保存できる記憶容量の爆発的向上が、統計を使って確からしい結果を導き出すことが出来るようになってきました。ここでいう「確からしい」というのは工学用語の方で、「きわめて確かっぽいけど、100%確実に正しいかどうかはわからない」という意味です。なぜそうなるかというと、何が正しいかという答えがないからですね。
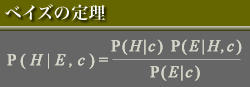
ベイズの方程式は上記ですがこれを非常にわかりやすく解説したサイトがありました。
こちらの初心者向け解説では非常に卑近な例を使ってわかりやすく解説しています。
デートの約束の時間に遅れた彼氏が、彼女を待たせています。彼女は怒っているかも知れません。遠くから見ると手を振ってニコニコしています。しかし過去の経験から顔は笑っていても怒っていることもあります。もしも怒っていると彼女の得意の真空とび膝蹴りを食らって治療費がかかります。これは花束でも買って怒りを鎮めた方がいいかも知れません。でも給料日前でかなり出費はイタイです。でも治療費の方がさらに高いです。この場合、どうしたらいいでしょう?
ここでベイズの方程式を使い、各項目に数値をあてはめて計算した結果、彼氏は彼女に花束を買う結果を導き出します。これなら早速応用してみたくありませんか!?
しかしこの状況で計算、しかも暗算できるのは東京大学物語の主人公くらいなものでは。遥ちゃーん。
おすすめ書籍:
評価が5点中5点!「マルコフ連鎖モンテカルロ法」というものが90年代流行って成果を収めているそうなので、これについても今後見てみたいです
aAa
画像を盗ってくるのは感心しないな
tnoma
大変失礼いたしました。画像は直リンクなので、コピーはしておりません。以降気をつけます。